State Space Models (2): networks and S4

Intro

Welcome to the second part of our State Space Model (SSM) series! In this post, we'll dive into how SSMs were initially incorporated into neural networks. We'll explore two key flaws in the first approach and how the S4 model addressed them. For context, here's a snapshot of where we are in the series:

• Part 1: Motivation and introduction to SSMs
  We go through where SSMs are right now, how they entered the machine learning landscape, and what they are.
• Part 2: SSM neural networks and Structured State Spaces
  We cover how SSMs were incorporated into neural networks, their shortcomings, and S4, an immediate successor and improvement.
• Part 3: State Space Selectivity (Mamba) and Duality (Mamba-2)
  We present Selective State Spaces and State Space Duality. Selectivity allows SSMs to focus on different parts of the input, like Attention. Speaking of, what's the relationship between SSMs and attention? In fact, they are surprisingly similar! What does this imply?

A bit of notation

As a reminder, here are the continuous $$ \begin{align} h'(t) &= \mathbf{A} h(t) + \mathbf{B} x(t) \label{eq:ssm} \\ y(t) &= \mathbf{C}h(t) \nonumber \end{align} $$ and discrete $$ \begin{align} h_t &= \bar{\mathbf{A}} h_{t-1} + \bar{\mathbf{B}} x_t \label{eq:ssm_dis} \\ y_t &= \bar{\mathbf{C}} h_t \nonumber \end{align} $$ SSM representations that we presented in the previous post. Let's formalize the dimensions of their parameters, as we need more rigor from this point forward:

A discrete SSM defines a map $x \in \mathbb{R}^{T} \rightarrow y \in \mathbb{R}^{T}$, where $T$ is the time dimension. That is, $x_t$ and $y_t$ are scalars. We also have the hidden state vector $h_t \in \mathbb{R}^{N}$, where $N$ is the state size, state dimension, state expansion factor, or even more. Parameters $\mathbf{A}$, $\mathbf{B}$, and $\mathbf{C}$ can be thought of as tensors of shapes $\mathbf{A} \in \mathbb{R}^{(N, N)}$, $\mathbf{B} \in \mathbb{R}^{(N\times 1)}$ and $\mathbf{C} \in \mathbb{R}^{(1\times N)}$. The discretization parameter $\Delta \in \mathbb{R}$ is a scalar. This notation will be changing as we move forward, so keep an eye on it.

With that out of the way, let's get going. Before we see how SSMs can be used in neural nets, we will see how the ways of computing them was characterized.

The Linear State-Space Layer

The vanilla SSM that we presented in the last post was generalized by Gu et al. (2021), and they called it the Linear State-Space Layer (LSSL). They characterized the LSSL in terms of its parameters, $\mathbf{A}$, $\mathbf{B}$, $\mathbf{C}$ and $\Delta$, and importantly by providing multiple interpretations of the model. These interpretations, or views, allowed us to define the same LSSL in different ways.

The three LSSL views

The authors of LSSLs argued that they could be viewed in three ways:

1. A continuous-time view, where the LSSL is just Equation $\ref{eq:ssm}$.
2. A recurrent view, where the LSSL was discretized like in Equation $\ref{eq:ssm_dis}$ and its operations were performed iteratively.
3. A convolutional view, where the LSSL was also discretized and its operations were defined as a convolution with a filter.

The first view we have already explored. If you noticed, the second and third views only differ from one another by how the output is computed. Let's address this, because it's essential.

LSSL: recurrent view

How would you implement the mechanical SSM simulation that we presented at the end of the previous post? Well, one could write down the parameters and create a function that given the previous hidden state and the current input, computes the next hidden state. Then, we could iterate this function over all inputs, each one depending on the last one. This is the recurrent view! It's just implementing Equation $\ref{eq:ssm_dis}$ naively.

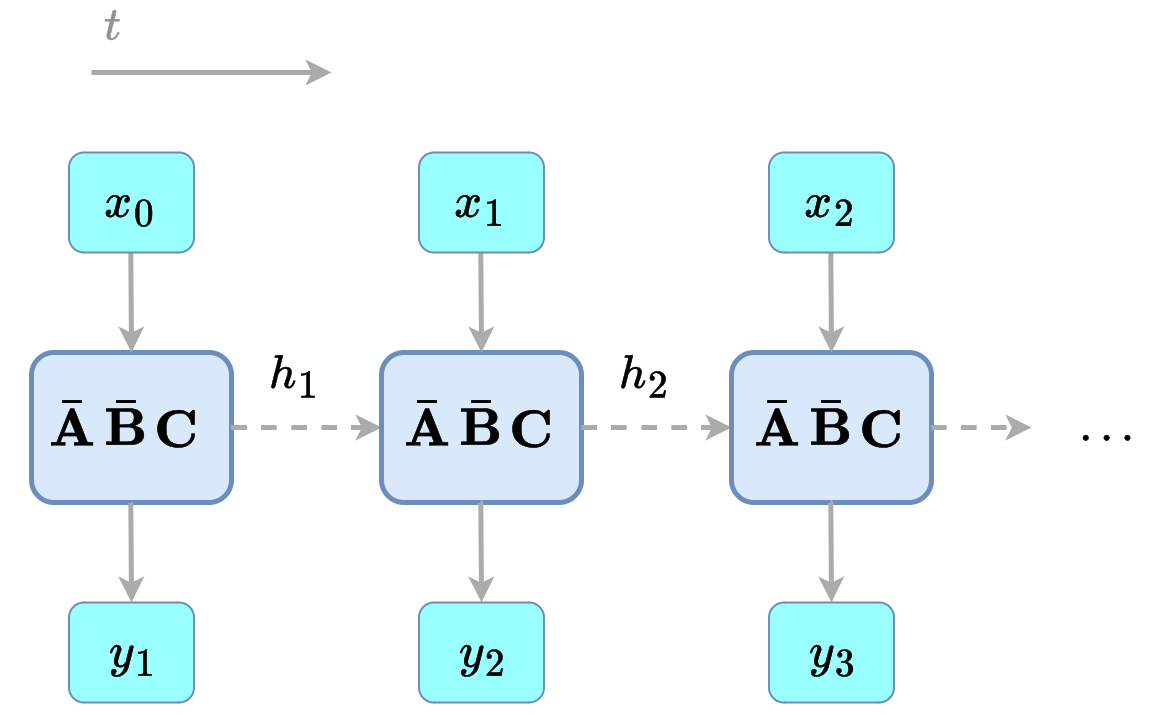
Figure 1: recurrent view of a discrete-time SSM.

This view is quite efficient. The amount of memory and computation used is the same in each step, and we only store the parameters, the previous state, and the current input. The downside is, it's sequential, so for a massive number of inputs, we will need to go one by one, without parallelization (a small lie, we will revisit this later).

You also may have noticed the similarities between the recurrent view of an LSSL and a traditional Recurrent Neural Network (RNN). Well, in the same paper, the authors showed that, actually, the RNN gating mechanism is analogous to the step size $\Delta$ in the LSSL. Not only that, they actually showed that LSSLs and RNNs like LSTMs, GRU, etc, all approximate the same type of dynamics. Neat!

Figure 2: recurrent view of an SSM (left) vs a vanilla RNN (right). Their parameters and operations are different, but they approximate the same dynamics.

LSSL: convolutional view

What's the other view? Well, if we pay closer attention to the recurrent view and write down how each step is computed, we can unroll the whole sequence. Following Equation $\ref{eq:ssm_dis}$, and assuming that $h_{-1} = 0$: $$ \begin{align} x_0 &= \bar{\mathbf{B}} x_0, & x_1 &= \bar{\mathbf{A}} \bar{\mathbf{B}} x_0 + \bar{\mathbf{B}} x_1, & x_2 &= \bar{\mathbf{A}}^2 \bar{\mathbf{B}} x_0 + \bar{\mathbf{A}} \bar{\mathbf{B}} x_1 + \bar{\mathbf{B}} x_2, & \ldots \nonumber \\ y_0 &= \bar{\mathbf{C}} \bar{\mathbf{B}} x_0, & y_1 &= \bar{\mathbf{C}} \bar{\mathbf{A}} \bar{\mathbf{B}} x_0 + \bar{\mathbf{C}} \bar{\mathbf{B}} x_1, & y_2 &= \bar{\mathbf{C}} \bar{\mathbf{A}}^2 \bar{\mathbf{B}} x_0 + \bar{\mathbf{C}} \bar{\mathbf{A}} \bar{\mathbf{B}} x_1 + \bar{\mathbf{C}} \bar{\mathbf{B}} x_2, & \ldots \nonumber \end{align} $$

We can see that this follows a pattern:

It can be shown that, given this expression, we can compute the whole output sequence $y$ with just an operation: the convolution. In particular, the convolution of the input sequence $x$ with what is called the SSM convolution kernel, or filter, $\bar{\mathbf{K}} \in \mathbb{R}^{T}$:

Figure 3: interactive SSM convolution view. Each filter element K(i) is multiplied by the corresponding input element. The results are summed to get the output y(i). Note how the kernel filter $K$ is as long as the input sequence ("A nice cat"). Also, see how each output element $y_i$ can be computed in parallel.

Now, as you may know, convolution is parallelizable, which is a huge plus versus the recurrent view. Because actually computing such a big convolution is unstable, we go further and, using the discrete convolution theorem, perform the operation by multiplying the Fast Fourier Transforms of the input $x$ and the filter $\bar{\mathbf{K}}$. We can then apply an inverse FFT to the result, making the operation more efficient. On the other hand, though, we see that the SSM filter is just as long as the sequence ($T$); its huge. This is a big downside, as we need to store all the parameters in memory.

Figure 4: Convolution using FFT.

So, these two views allow us to compute the same output in different ways:

• The recurrent view is memory and compute efficient, but sequential.
• The convolutional view is memory heavy but can be parallelizable.

We are finally ready to see how SSMs can be incorporated into neural networks.

SSM neural networks

How do we stack LSSL blocks so that we end up with a model with the same signature as modern neural networks? Well, an LSSL block maps a scalar to a scalar, but what if we want to map a scalar to a vector? Or a vector to a vector? In that case, we need to add a head dimension $P$. Intead of having a single LSSL block, we can stack $P$ blocks, each mapping the input to a different output. These blocks may share parameters ($\mathbf{A}$, $\mathbf{B}$, $\mathbf{C}$ and $\Delta$), or each be trained independently.

Formally, we now may interpret input $\mathbf{X} \in \mathbb{R}^{(T, P)}$, with $P$ LSSLs stacked independently (heads), having output $\mathbf{Y} \in \mathbb{R}^{(T, P)}$. We may also have input $\mathbf{X} \in \mathbb{R}^{(T)}$, with $P$ LSSLs stacked, having output also $\mathbf{Y} \in \mathbb{R}^{(T, P)}$ (each input goes through $P$ LSSLs). The lesson here is that we can stack LSSL blocks to create a model that maps a sequence to another sequence, with the same signature as a modern neural network.

Figure 5: Multi-head SSM. The input signal can either be repeated or have multiple dimensions.

We can then get this stack of LSSLs and add normalization before it, and dropout, activation and a skip connection after it (an example). Voilà, this is looking more like a neural network layer. We can even connect many of these layers one after the other to finally get something analogous to a deep learning model. This can be used for classification or generation, just like a Transformer. Note that only parameters $\mathbf{B}$, $\mathbf{C}$ and $\Delta$ are learnable. $\mathbf{A}$ is fixed and will need to have a particular structure.

Figure 6: zoom-in of an example SSM layer (top), part of a larger network (bottom).

LRD & HiPPO

Given how we have defined SSMs until now, and even with the SSM neural network design, there is a big problem. They were shown to have limitations when trying to remember long-term dependencies (remember LRD data?). Let's address this.

Happy HiPPO: enabling long-term context

As we have seen, the $\mathbf{A}$ matrix is the one that defines how the previous state influences the current one (expressions \ref{eq:ssm} and \ref{eq:ssm_dis}). One interpretation of this is that the $\mathbf{A}$ matrix compresses the information of the past into the current state. If we have a random $\mathbf{A}$ this compression is going to be bad, and previous context will vanish. Well, let's learn $\mathbf{A}$! Still, not only is it expensive, it's also not enough. Well, then, is there any way to give $\mathbf{A}$ a structure that helps it compress the information better without having to train it? Introducing the HiPPO matrix!

HiPPO (2020) (High-Order Polynomial Projection Operator) defines a class of matrices that, in our case, allow continuous-time memorization of the state $h(t)$. Using what's called as the HiPPO matrix as $\mathbf{A}$ enables the history of the state to be compressed in a way that can even be approximately reconstructed. Just the change of a random inicialization of $\mathbf{A}$ to a HiPPO matrix improved MNIST classification of an SSM from $60\%$ to $98\%$ accuracy!

A HiPPO matrix has a specific structure: $$ \mathbf{A}_{nk} = \begin{cases} (2n + 1)^{\frac{1}{2}} (2k + 1)^{\frac{1}{2}} & \text{if } n > k \\ n + 1 & \text{if } n = k \\ 0 & \text{if } n < k \end{cases} $$ And although the claims are nothing short of amazing, they are also a bit math heavy. They entail Legendre polynomials, and going into detail would probably make this too long. Intuitively, though:

1. The matrix makes each hidden state value $h_i$ approximate a coefficient $c_i$.
2. For each value of $i$, a unique function exists (the $i_{th}$ Legendre Polynomial).
3. We use the sum of each Legendre polynomial, weighed by their respective coefficient, to approximate the state history.
4. Each step, the coefficients (again, values of hidden state) are updated by the HiPPO matrix $\mathbf{A}$. So, the state history gets updated.

Figure 7: reconstruction of the state history via Legendre polynomials. $c_i$ (which would be the $h_i$) adjusts how much each Legendre polynomial (in blue) contributes to the reconstructed state history (in red). To show a clear distinction, shown are the $4_{th}$, $10_{th}$ and $28_{th}$ Legendre polynomials, top down.

Alas, even with HiPPO matrices, problems still plague these lands. Now, although a deep LSSL network can perform well on LRD, it has prohibitive computational and memory requirements, mainly due to the state representation (not on the recurrent view, as the requirements are constant). If we want these models to be competitive to comparably-sized RNNs, we need to dig further. Luckily, just one trick does it!

Structured State Spaces

In 2022, Structured State Spaces (S4) were introduced. In S4, the authors basically showed how to address the computational and memory issues that we mentioned previously. As we said, the issues mainly came from how the convolutional view, which was the one needed for training, required computing and keeping in memory the huge filter $\bar{\mathbf{K}}$.

If we look at Equation $\ref{eq:conv_filter}$, we notice how not only there is lots of parameters to store, but also how we need to compute powers of $\mathbf{A}$. This is a red flag. Motivated by the properties of diagonalizable matrices, S4 finds a way to represent the HiPPO matrix $\mathbf{A}$ so that the filter $\bar{\mathbf{K}}$ can be computed fast, and with less memory. In the end (and after a lot of math), they end up decomposing $\mathbf{A} = \mathbf{\Lambda} - \mathbf{P} \mathbf{Q}^*$ into its diagonal $\mathbf{\Lambda}$ and vectors $\mathbf{P}$ and $\mathbf{Q}$, all learnable but initialized from a HiPPO matrix. Overall, then, now we can say that $\mathbf{A} \in \mathbb{R}^{N}$. Not only that, its powers can be computed very fast and the prohibitive costs for computing the convolutional view are now gone. Again, sorry for not going into detail; sources are already amazing (paper, The Annotated S4)

Although the change presented here may seem complex, it only changes how the SSM is parametrized ($\mathbf{A}$ is substituted by $\mathbf{\Lambda}$, $\mathbf{P}$ and $\mathbf{Q}$). Updating how the filter $\bar{\mathbf{K}}$ is computed is the only change needed. This is a big win, as the rest of the model, and so the neural network design, remains the same!

Next up

In this post, we explored ways to view an SSM, how we can use it for inference and train it, how it can be incorporated into a neural network design, and how to address its computational and context limitations. In the next post, we will fix yet another shortcoming: linear-time-invariance. We will see what Mamba is and how to make SSMs focus on different parts of the input, just like attention mechanisms do. We will also establish a relation between SSMs and attention and present Mamba-2.

Citations

If this has been useful and you want to cite it in an academic setting, please use the following bibtex. ❤️

@misc{chus2024SSM,
      author = {Jesus M. Antonanzas},
      title = {State Space Models: from 0 to Mamba-2},
      year = {2024},
      howpublished = {\url{chus.space/blog/2024/ssm_1_context}},
      note = {P1: intro to SSMs; P2: nets & S4; P3: Mamba & Mamba-2}
}

References