State Space Models (3): Mamba & Mamba-2

Intro

Welcome back to the SSM series! This is part 3 of 3, where we finally talk about the Mamba family of models: Mamba and Mamba-2 at the time of writing. If you haven't read the previous parts, I recommend you do so before continuing.

• Part 1: Motivation and introduction to SSMs
  We go through where SSMs are right now, how they entered the machine learning landscape, and what they are.
• Part 2: SSM neural networks and Structured State Spaces
  We cover how SSMs were incorporated into neural networks, their shortcomings, and S4, an immediate successor and improvement.
• Part 3: State Space Selectivity (Mamba) and Duality (Mamba-2)
  We present Selective State Spaces and State Space Duality. Selectivity allows SSMs to focus on different parts of the input, like Attention. Speaking of, what's the relationship between SSMs and attention? In fact, they are surprisingly similar! What does this imply?

If you read the previous posts, by now you should understand:

• how a basic SSM block works.
• how SSM blocks can be represented in different ways. Each interpretation (recurrent, convolutional) is equivalent in functionality but has different characteristics, making one preferable over the other in certain contexts.
• how SSM blocks could be stacked and organized to create a sequence mapper with the same signature as a common neural network.
• what enables SSM blocks to have long term memory (the HiPPO $\mathbf{A}$ matrix).
• how the memory footprint problem of the convolutional view of an SSM is mitigated (structured state spaces).

In summary, based on what we know now, one could very well create a performant (both in predictive capabilities and resource requirements) SSM-based model capable of competing with similar, more traditional methods.

There is a particular technique that is now ubiquitous, though, and which we have not used for our comparisons yet. Let’s address the elephant in the room: can all this even really begin to compete with what the attention mechanism can do? Let's see how the authors of Mamba and Mamba-2, Albert Gu and Tri Dao, did it.

Attention, please

Although something similar to attention existed before 2017, Vaswani et al. made it popular with Attention Is All You Need. The Transformer caught the world by storm and changed the deep learning landscape. Why? Because Attention enabled the model to select which parts of the input, or even intermediate steps, could be useful for each prediction. This is called selectivity. Now, selectivity meant that the behavior of the model would not always the same, in the sense that different operations would be performed by the model depending on the input. To predict the word that comes after the sequence “All felines are cool, and so is my _” the model would not consider all words in the sequence uniformly useful, but rather it would probably understand that the sequence refers to felines in particular and thus predict “cat” as the next word. There are a million resources on attention, so I won’t go into more detail here.

Now, if we refer to our current formulation of an SSM block, we see how all matrices ($\bar{\mathbf{A}}$, $\bar{\mathbf{B}}$, $\bar{\mathbf{C}}$) are static: $$ \begin{align} h_t &= \bar{\mathbf{A}} h_{t-1} + \bar{\mathbf{B}} x_t \label{eq:ssm_dis} \\ y_t &= \bar{\mathbf{C}} h_t \nonumber \end{align} $$ That is, whatever the input $h_t$ is, the same operations are always performed. Thus, selectivity cannot occur right now, as there is no way for our models to discern what is useful and what is not. More formally, they are linear time invariant (LTI).

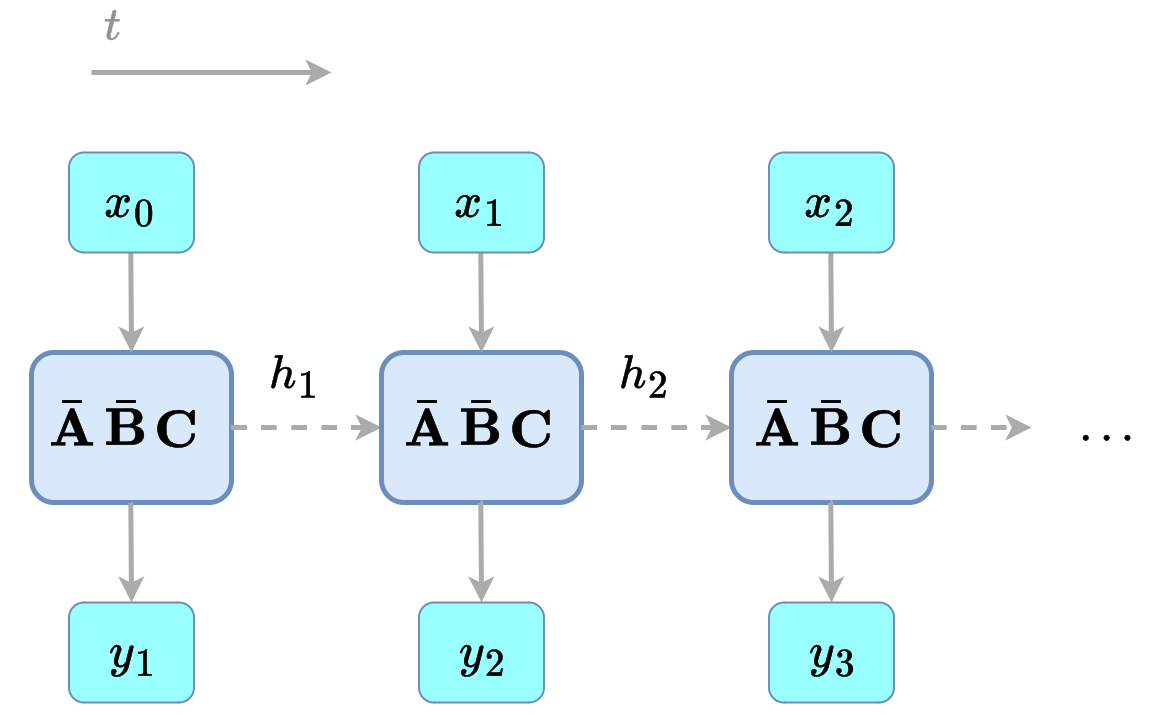
Figure 1: the same parameter matrices are used regardless of the input. Borrowed from the first part of the series.

So, if SSMs are to become equally as capable as our current state of the art models, they need to be selective! This was the main contribution of Mamba, along with implementation details and some optimizations. Let's see how they did it.

Mamba: selectivity in SSMs

Motivation: selection as a means of compression

With a (naive) Attention implementation, all key and value representations of all parts of an input are saved in memory. Naturally, this much information allows for a powerful way of selecting what is useful and what is not, at every moment. However, this also means that the memory footprint of the model is very large (many advances have been made). This is effective but inefficient, as nothing is compressed.

On the other hand, when a vanilla SSM block or RNN is used, the hidden state compresses all input information up to the current part into a fixed-size vector. This is efficient, but not effective, due to indiscriminate compression.

Now, because SSM blocks use a fixed-size hidden state, there will always be compression. For an effective compression, though, the model needs to be able to select what is useful and what is not: selection as a means of compression. Thus, a fixed hidden state coupled with selection will help us better explore this effectiveness-efficiency tradeoff.

Figure 2: how information is compressed determines the effectiveness and efficiency of a model.

Parameters as functions of the input

How can we make SSM blocks selective? A related question for the reader is: what parameters, from equation $\ref{eq:ssm_dis}$, influence how information propagates and how the output is constructed? The answers are (1) all matrices that update the hidden state ($\bar{\mathbf{A}}$ and $\bar{\mathbf{B}}$), and (2) the $\bar{\mathbf{C}}$ matrix. If we want SSMs to be selective, that means that they need to behave differently depending on the input. That is, parameters that control the dynamics need to be input-dependant.

For this, the Mamba authors propose a simple solution: create parametrised (trainable) functions that map the input in each timestep to the corresponding parameter matrices. These functions exist for each parameter that needs to be selective. For example, if we want the $\bar{\mathbf{B}}$ matrix to be selective, we train, as part of the SSM block, the linear projection $s_B(x) = $Linear${}_N(x)$ that maps the input $x$ to the $\mathbf{B}$ matrix. This way, the $\bar{\mathbf{B}}$ matrix will have a different structure depending on the input and will selectively interact with information.

Figure 3: parameters $\mathbf{B}$, $\mathbf{C}$ and $\Delta$ are now linear projections of the input $x_t$.

Note how, in the previous paragraph, the linear map outputs the undiscretized matrix! To be precise, the Mamba paper proposes to make $\mathbf{B}, \mathbf{C}, \Delta$ functions of the input: $$ \begin{align} \mathbf{B} &= s_B(x) \nonumber \\ \mathbf{C} &= s_C(x) \nonumber \\ \Delta &= \tau_{\Delta}(p + s_{\Delta}(x)) \nonumber \end{align} $$ where $p$ is a fixed parameter and: $$ \begin{align} s_{\Delta}(x) &= \text{Broadcast}_T(\text{Linear}_1(x)) \nonumber \\ s_B(x) &= \text{Linear}_N(x) \nonumber \\ s_C(x) &= \text{Linear}_N(x) \nonumber \\ \tau_{\Delta} &= \text{Softplus} \nonumber \end{align} $$ where $T$ is the size of the input sequence (time dimension), and $N$ is the state size. Again, the main idea is that the matrices are functions of the input, and that the input is mapped to the matrices by linear functions. The $\Delta$ matrix is constructed like that because, as the authors show, it's actually a nice generalisation of RNN gating.

An important clarification to make is why the $\mathbf{A}$ matrix is not a function of the input, but a fixed parameter. Look at equation $\ref{eq:ssm_dis}$ and again think about the roles of each matrix. $\bar{\mathbf{A}}$ enables memorization of the hidden state, $\bar{\mathbf{B}}$ determines how the input influences the state, and $\bar{\mathbf{C}}$ how the state influences the output. The purpose of selectivity is for the model to be able to focus on different parts of the input. Thus, the influence of the previous hidden state on the current one should remain a fixed operation, rather than being selective. If you don't find this argument compelling enough, also note how the only way $\mathbf{A}$ interacts with the system is via $\bar{\mathbf{A}} = e^{\Delta \mathbf{A}}$ (the discretization, which we address in post 1 of the series). Thus, one could argue that selectivity in $\Delta$ is enough for $\bar{\mathbf{A}}$ to be selective.

The importance of implementation

With the change of making some parameters input dependent, the ability to express an SSM as a convolution (see previous post) is lost: the kernel is not fixed anymore. Thus, we only have the recurrent view of an SSM block, which is not as efficiently computed as the convolutional view when expressed naively. A big contribution of the Mamba paper, on top of the actual idea, is the implementation of the selective SSM block. With it, they address the following problems:

1. Parallelisation of the recurrent view.

2. Memory limitations.

Let's get into it.

Mamba: making it practical

The Mamba paper is a wonderful piece of research. While many of the ideas are not new, a special kind of mind is required to bring them together and implement them in harmony. Had the authors not included an efficient implementation of the selective SSM block, Mamba would have been impractical for real world use. So, in this section, I want to briefly lay down the intuition behind what I consider two of the most relevant implementation details. For further reading, I strongly recommend this post by James Chen.

The Blelloch parallel scan

For the training of Mamba to be efficient, we need to parallelise it. The Blelloch parallel scan algorithm has been relatively recently used for parallelizing RNNs, and if you have been paying attention, something in you might tell you that it may be possible to also apply it to State Space Models. Well, that's exactly what happened!

As its name suggests, the parallel scan algorithm is used to perform an operation called a scan in parallel. In short, the scan iteratively and cumulatively applies an operator to a list. This scan operation can actually be used to express how recurrent models compute hidden states:

Figure 4: scan operation in two contexts. Left: the basic sum scan over a list of 4 elements (top) and the resulting object (bottom). Right: A conceptual scan operation to compute each state $h_t$. The operator $?$ represents an unknown, which I talk about below. $\overline{A}_i$ and $\overline{B}_i$ represent the discretized parameter matrices of each timestep $i$. The actual scan operation is different, but this helps illustrate the point: it's a scan.

As you can see in Figure 4, the state $h_t$ is not computed with just sums. Well, the parallel scan algorithm doesn't just work with the sum operator, but with all binary (input two numbers, output one) and associative (the order does not matter) operators! So, if we can design an operator for Mamba that meets these properties, we can parallelise the scan (refer to James Chen's post as mentioned before). As a spoiler, the resulting operator is a way to express how $\overline{\mathbf{A}_t}$ and $\overline{\mathbf{B}(x_t)}x_t$ are computed at any point in time in the sequence $t$. With the matrices available, follow equation $\ref{eq:ssm_dis}$ to see how $h_t$ is computed. This is sufficient for applying the Blelloch algorithm, thus parallelising the training of Mamba.

As a sidenote, this parallelisation is also useful at inference time, but not as much given that requests will come asynchronously. At that point, it becomes a problem of batching and scheduling.

Hardware-aware computing

Nowadays, a lot of software is developed without taking any target hardware into account. In spite of this, for certain applications, there are plenty of benefits of knowing how the hardware your application is going to run on works.

You might recognize one of the Mamba authors, Tri Dao, by his work on FlashAttention. FlashAttention is an implementation of the attention mechanism that drastically reduces the amount of memory transfers between High-Bandwidth Memory and SRAM, from where the processor units pull the data for performing operations. They way this is done is out of the scope of this post, but the main idea is that because Attention is memory-bound (more time moving things around than actually doing computations), the less memory transfers, the faster the model. This is a hardware-aware implementation.

Figure 5: memory and compute intensity of random processes. Given constrained resources, processes in the upper left will be memory-bound, while those in the lower right will be compute-bound.

The authors recognised that Mamba was memory-bound and did the same: reduce the amount of memory transfers. The usual flow for a GPU program is:

1. Load data from HBM to SRAM.
2. Compute.
3. Store results from SRAM to HBM.

Figure 6: a demonstration of kernel fusion for the operation $A + B*C$. Left: no kernel fusion. Right: kernel fusion. The operation is for illustrative purposes: no kernel fusion requires more byte movement between memory layers.

Another technique that they use to make the selective SSM block efficient is recomputation, which means to avoid storing objects that are needed later on (such in the backward pass) in memory and instead compute them again. When an operation is clearly memory-bound, this makes everything go faster.

In conclusion, the selective SSM block is implemented efficiently mainly by:

• Parallelising the scan operation with the Blelloch algorithm.
• Using hardware-aware computing techniques such as kernel fusion and recomputation.

The Mamba block

Just as we described in post 2, the SSM block is not the only ingredient for a succesful model. We saw how one could combine multiple SSM blocks with traditional operations such as softmax or linear projections to build a "neural network" with SSMs as a core. Mamba is no different: in the paper, the selective SSM block is combined with multiple other operations to form a complete Mamba block. This can then be combined with other Mamba blocks to create a full deep network.

In conclusion, a Mamba block is a selective SSM block combined with other deep learning operations, which is then stacked to create the Mamba model. To increase performance, the authors introduce hardware-aware techiniques such as kernel fusion and recomputation. The result is a model that can be trained and run efficiently on modern hardware.

Figure 7: the Mamba Block. In peach are nonlinearities (multiplication, activation), in blue linear projections and in green sequence transformations.

Mamba-2: an overview

If you have read through all three posts (thank you so much!), you might have noticed that this journey is one of improvements. From plain vanilla state space models to deep networks, through state history reconstruction and hardware-specific optimizations to selection mechanisms, we have been incrementally building upon the previous iteration. Mamba and Mamba-2 were published in relatively quick succession, and although the practical changes introduced by Mamba-2 were not many, a rich theoretical framework was presented along it. This framework enabled the authors to characterize the relation of SSMs to attention. So, SSMs can be viewed through different lenses: as continuous, recurrent, convolutional and attention-based models!

In this section, I want to very briefly summarise the practical changes and the theoretical conclusions presented by the Mamba-2 paper. The theoretical framework is perhaps the most important result from the paper, and because this series focuses more on the models, I will be skimming through. Visit the great Mamba-2 original blog posts for the best in-depth presentation of the topic. In spite of all this, we need just a bit of theoretical intuition to contextualise the practical results.

Overview of the State Space Duality framework

Before deriving the relationships between attention and state space models, the authors explore the properties of both from the perspective of structured matrices (they both worked with them at the beggining of their PhD's, so it's a natural choice):

• as for Structured State Space Models, they show an equivalence with semiseparable matrices. From this formulation, the authors show that SSMs can be computed in two ways: a linear, recurrent one via tensor contractions (as usual), and a quadratic (naive) one via pure matrix multiplications.
• as for attention variants, they define structured masked attention (SMA), which is another generalisation. With this, they show that quadratic (the usual) and linear attention are simply different orders by which to compute masked attention via tensor contractions.

Figure 8: Structured State Space Duality. SSMs and Attention can be studied from the perspective of Structured Matrices via semiseparable matrices and SMA, respectively. This unlocks the State Space Duality between both. From the Mamba-2 paper.

So, from both a SSM and an attention perspective, we now have the same two ways to compute them: a linear and a quadratic one. In fact, both turn out to be different perspectives on the same duality. When constructing an SSM and an attention variant in a particular way, they have the exact same linear and quadratic forms, and are thus equivalent! This is the Structured State Space Duality (SSD). As for the special cases, they are the following:

• as for SSMs, when $\mathbf{A}$ is a scalar times identity matrix (all elements in the diagonal are the same).
• as for attention, when it's masked and the mask is what they call a 1-semiseparable matrix. We are not that interested in this instantiation because we only implement the SSM case.

Figure 9: To the left, a scalar times identity matrix. To the right, a 1-semiseparable matrix.

Let's see what this duality actually implies for our current SSM implementation.

The consequences of State Space Duality

Motivated by their strong theoretical findings, the authors went on and implemented the special SSM case (scalar-identity $\mathbf{A}$ matrix) as the new core of Mamba-2. They now call this core the SSD model, and plays the same role as an SSM block: can be stacked and combined with other operations to create a neural network. Another change, not in the SSD model itself, but in how its used to deal with inputs $x_t$ with dimension $\gt 1$: use the same SSD model (same $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$ matrices) for each dimension.

These two changes allow the SSD model to be expressed in its quadratic form by following the SSD framework. This enables the creation of a new algorithm to compute the model, which they call "SSD algorithm". It uses the FLOPS of SSMs (scales quadratically with input dimension, not sequence length as does Attention), and expresses the model as matrix multiplications just like Attention, thus being more hardware-efficient than SSMs. For completion, two more changes changes introduced in Mamba-2 w.r.t Mamba that we have not discussed are:

• the $\mathbf{A}$, $\mathbf{X}$, $\mathbf{B}$ and $\mathbf{C}$ matrices are produced by a single projection at the beginning of the SSD block instead of as a function of $\mathbf{X}$ (in the case of $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$). This enables better Tensor Parallelism (like in Megatron).
• added a normalisation layer before the last linear projection of the block, which increases stability.

Figure 10: The Mamba-2 block. In peach are nonlinearities (multiplication, activation, normalisation), in blue linear projections and in green sequence transformations. Note how similar it is to the original Mamba block.

So, all of the theoretical developments have allowed us to develop a model that can be computed much more efficiently, both in memory and compute terms, than the original Mamba, with (approximately) the same predictive performance. A "restriction" on the original Mamba that allowed it to train up to 50% quicker and have 8 times bigger states given the same memory footprint. That's Mamba-2.

Series conclusion

And this is the end of the SSM series! What I personally find most interesting about the Mamba-2 paper is that it showcases the depth and breadth of skills of the authors: first, they introduce a new theoretical framework, then they apply it to create a new algorithm, and finally they create a whole bunch of optimizations for real world training and inference systems.

During this series, I have introduced a lot of concepts, and I hope that you have been able to follow along. Of course, what I have presented is just a narrow view of the state and evolution of the field, with many interesting papers and ideas left out. If this has sparked your interest, I recommend that you keep up with the latest research in the field: I have a hunch that the theoretical framework introduced in Mamba-2 will be used in many interesting ways, especially with how it unifies SSMs and attention. The biggest question for me is what (and if) other models can be unified with this framework, and what algorithmic discoveries will it bring. The field of deep learning is notorious for introducing innovations that are not really understood from a theoretical perspective, and I think that the SSD framework is a step in the right direction.

Writing this has been a blast. I hope you have enjoyed reading it as much as I have enjoyed writing it. If you did, sharing it would mean a lot to me. If you have any questions, comments, or suggestions, please don't hesitate to reach out. Until next time!

Citations

If this has been useful and you want to cite it in an academic setting, please use the following bibtex. ❤️

@misc{chus2024SSM,
      author = {Jesus M. Antonanzas},
      title = {State Space Models: from 0 to Mamba-2},
      year = {2024},
      howpublished = {\url{chus.space/blog/2024/ssm_1_context}},
      note = {P1: intro to SSMs; P2: nets & S4; P3: Mamba & Mamba-2}
}

References